Top > Others >> 元の位置に戻る >>> 経度、緯度について詳しく
経度や緯度(まとめて経緯度といいます)については中学校で学ぶようですが、ここでは復習も交えて少し詳しく見てみましょう。
なお、このページのほとんどの図はブラウザ画面幅の 80%で表示しています。環境によっては表示速度が遅くなる場合がありますが、ご了承下さい。
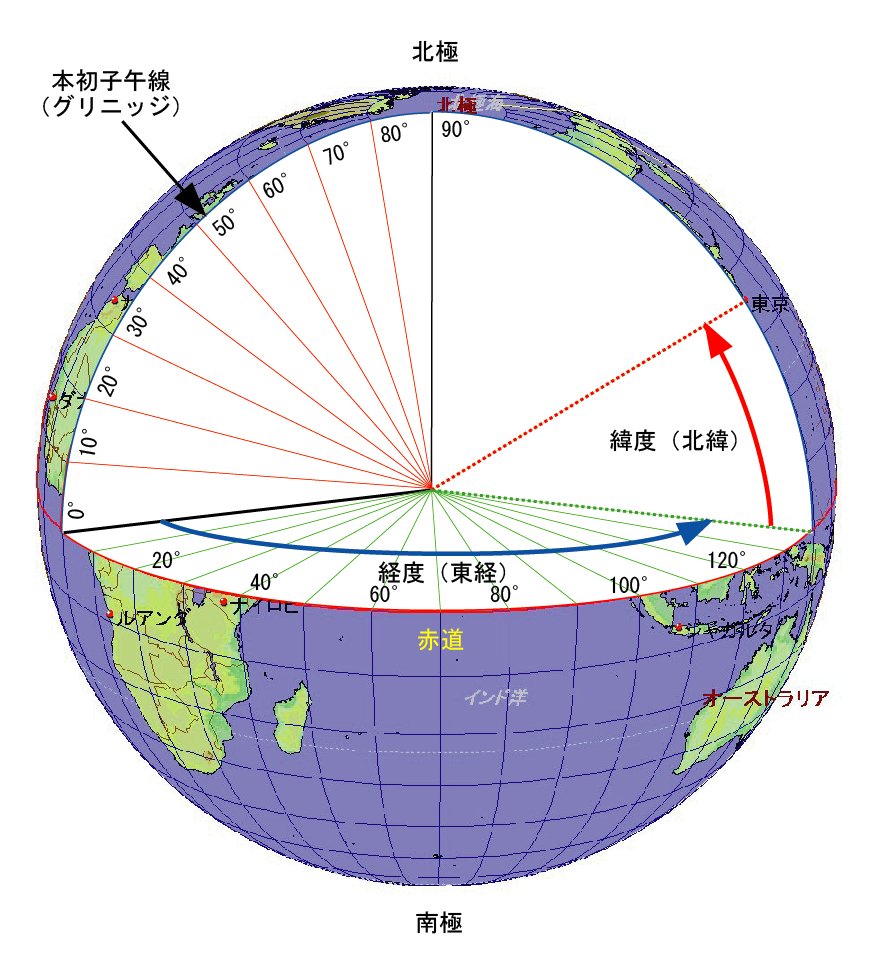
そもそも経緯度は、地球上の任意位置を指し示す手段として考え出されました。下の図のように、地球の南北の中心に赤道があることはご存じですね。南北の位置を特定できる緯度は、この赤道を基準に決められています。
Point
緯度は赤道を 0度とし、南北それぞれ 90度に分け、北を北緯、南を南緯として数える
日本は赤道より北(北半球)にありますから、北緯○○度△△分と表すのが常で、東京は、おおよそ「北緯 35度 41分」(「北緯 35゜41.00’」)で、航海計画での表記法は、「35゜ -41.00’N 」となります。この表記の中で、「゜」と「’」の間に「-」(ハイフン)が入ります。区切り記号ですので、「−」(マイナス)と勘違いしないよう注意しましょう。同じ緯度を結んだ線を「緯線」(または緯度線、平行圏)とよびます。

緯度の基準が赤道であることは前述した通りですが、東西方向の位置を特定できる経度の基準は 1884年の「万国子午線会議」で統一されるまで各国バラバラだったようです。子午線(しごせん)とは地球の両極を結ぶ線で、十二支の「子(ね)」(方角で北)と「午(うま)」(方角で南)から命名されています(英語では Meridian)。経度の起点としては、どの子午線を使っても良いのですが、国際的に統一していないと不便であるとの理由で、1884年、万国子午線会議において、ロンドンのグリニッジ(Greenwich)にあった「旧王立グリニッジ天文台」を通る子午線を起点と定めました。これが本初子午線です。
Point
経度は本初子午線を 0度とし、東西それぞれ 180度に分け、東を東経、西を西経として数える
日本は本初子午線より東 180゜以内にありますから、東経○○○度△△分と表すのが常で、東京は、おおよそ「東経 139度 46分」(「東経 139゜46.00’」)で、航海計画での表記法は、「139゜ -46.00’E 」となります。同じ経度を結んだ線を「経線」(または経度線、子午線)とよびます。
球体である地球の表面を完全に模写するには地図も球体である必要があります。これを実現したのが地球儀と言えるでしょう。地球儀は地球のイメージをほぼ正確に表現していますが、航海などの実用では取り扱いに不便があります。
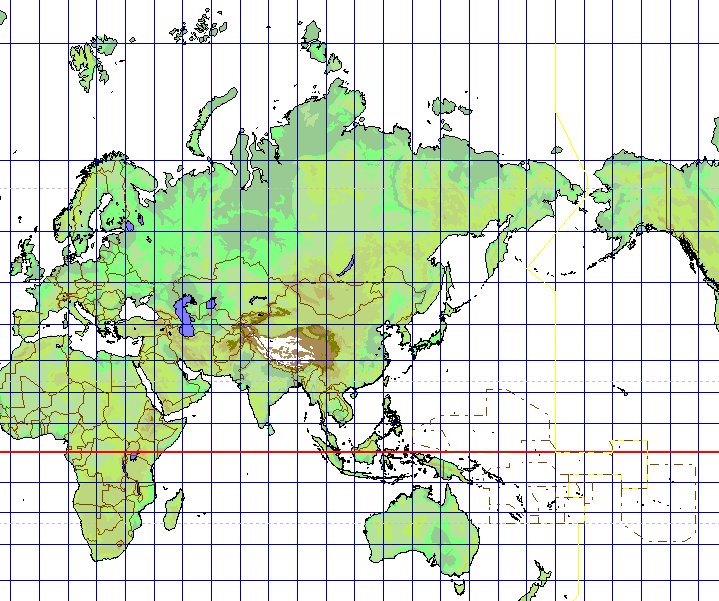
そこで、地球を平面に描写する「地図の投影法」が幾つか考案されました。航海には「メルカトル図法」(1569年、オランダの地理学者メルカトルの考案)が用いられます。メルカトル図法は地球の赤道のみが接する円筒内に地球を置き、経緯線を円筒に投影してから円筒を開いて地図を描く「円筒図法」に数学的な補正を施した「正角円筒図法」に分類されます。メルカトル図法では赤道に近い地域は正確に描写されますが、高緯度になると大きく歪む欠点があります。上の地図のように極に近づくほど緯線の間隔が広くなり本来の形状から歪んだ地形となります。しかし、二点間の方位を正しく示すことから、航海で針路を特定するにはメルカトル図法が最も適しています。
海図の四方には経緯度を示す「経度目盛」と「緯度目盛」が印刷されています。この経緯度目盛を使用して船位を特定したり、船位から経緯度を計測することができます。ここでは、経緯度目盛の読み方を見てみましょう。
経緯度目盛を読む前に角度について復習しておきます。経緯度は基線からの角度で表されることは前述しました。この角度は円を 360で分割した 1度(1゜)が元単位となりますが、使用上は 1度を更に 60等分した 1分( 1’)、1分を更に60等分した 1秒( 1”)を用います。航海計画では秒の単位は使わず、「30゜ -02.5’N」のように小数第1位までの分単位で表します。
Point
1゜= 60’ (1度=60分)、 分は小数第1位まで使用
度と分の関係から、航海計画を扱う問題の計算結果が小数を含む「○○.△△゜」のようになった場合、「○○゜☆☆’」のように書き直すことができます。
具体的には、 0.5゜= 0.5×60 = 30’のように、度の小数部分に「60」を掛けると分の単位にすることができます。したがって、12.3゜= 12゜+ 0.3×60 = 12゜-18’となります。
Point
度の小数部分に 60を掛けると分になる (例)24.75゜= 24゜+ 0.75×60 = 24゜-45’
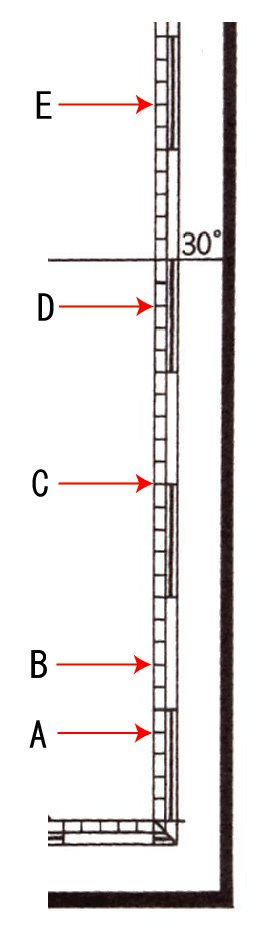 それでは、以下の経緯度目盛を読むことにしましょう。海図上の経緯度線は10’毎に引かれ、 1’毎に白黒目盛、0.2’毎に最小目盛が印刷されています。経緯度目盛上の数値表示は、10’ごとにしか記入されていませんが、海図の左下に海図の起点となる経緯度が示されているので、これを元に経緯度を読みます。この起点の経緯度表示は経緯度が逆さまに記されているように見えるので、混乱しないよう注意します。
それでは、以下の経緯度目盛を読むことにしましょう。海図上の経緯度線は10’毎に引かれ、 1’毎に白黒目盛、0.2’毎に最小目盛が印刷されています。経緯度目盛上の数値表示は、10’ごとにしか記入されていませんが、海図の左下に海図の起点となる経緯度が示されているので、これを元に経緯度を読みます。この起点の経緯度表示は経緯度が逆さまに記されているように見えるので、混乱しないよう注意します。
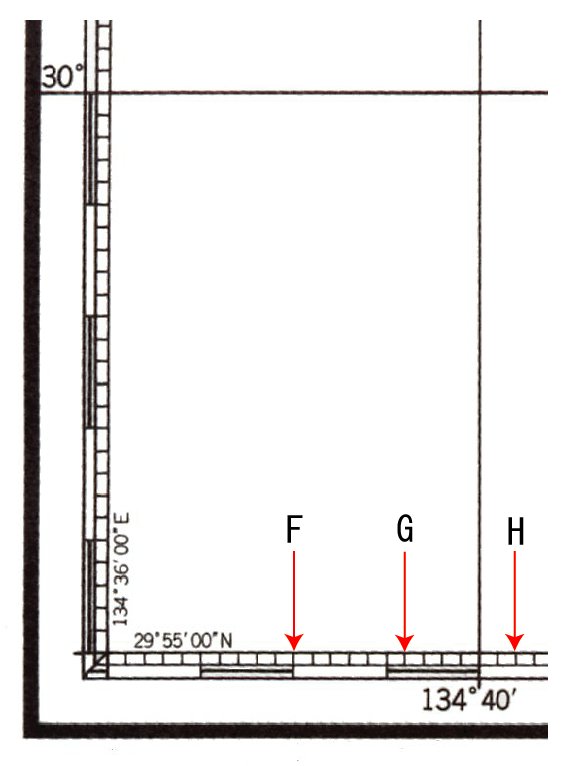
では、上図のA〜Eの緯度、F〜Hの経度を順に読んでいきます。分からない場合はポイント欄を参照してください。起点の経緯度は「29゜55’00”N」「134゜36’00”E」です。
| 記号 | 経緯度 | ポイント |
|---|---|---|
| A | 29゜-55.8’N | 起点の緯度は 29゜55’00”N 最小目盛は 0.2’ |
| B | 29゜-56.4’N | 29゜56’と 0.4’ |
| C | 29゜-58.0’N | 29゜58’ちょうど |
| D | 29゜-59.6’N | あと 4’で 30゜00.00’になります |
| E | 30゜-01.4’N | 最初の白黒目盛は 30゜-1.0’N |
| F | 134゜-38.0’E | 起点の経度は 134゜36’00”E |
| G | 134゜-39.2’E | あと 8’で 134゜40.00E |
| H | 134゜-40.4’E | 134゜40.00E から 0.4’ |
緯線(横の線)が作る円は赤道が最大で高緯度になるほど小さくなるので、経度目盛を距離の測定に使うことはできません。一方、経線(縦の線)は全ての子午線が大円(球の中心を通る円)となるので、緯度目盛を距離の測定に使用することができます。厳密には地球は完全球ではなく、南北に扁平であるので、緯度 1゜に相当する距離は赤道付近で 110.57km、極付近で 111.70kmと、1km強の違いがあります。しかしながら、これ程の違いは航海上で問題となるものでなく、航海計画でも緯度目盛を使用して距離の測定を行います。参考までに、経度 1゜は赤道上で 111.32kmになります。
Point
海図上では緯度目盛を距離測定に用いる 経度目盛は使わない
緯度と距離との関連を示すと次のようになります。
Point
緯度 1’(分)= 1海里(かいり、マイル、nautical mile、記号 NM、nm、M) 1海里 = 1852m
海図を用いて航海する場合、距離単位に緯度と密接な関係にある海里を使うと非常に便利であるので、航海ではもっぱら海里を用いることになっています。海図の右側の緯度目盛には「km目盛」も併記されていますが、航海計画では使用しません。
1海里が 1852mであることは、1929年の国際水路会議で取り決められました。日本はこれを批准していますが、英米のように国によって多少の違いがあるようです。1海里 1852mというのは中途半端な数字ですが、前述したように海図上の距離は緯度と相関であることから、子午線を通る円周長を 360゜で分割し、更に 60等分すると緯度 1’の距離が算出できます。逆算すると、1852m × 60 × 360 = 40003200m = 40003.2km ≒ 4万km となり、地球の大体の大きさが推測できます。
自動車の速度は1時間当たりの走行距離(km/h、時速)で示すことが多い(日本では)と思いますが、海上では 1時間当たりの航走距離(海里)を示すノット(KN、knot)という単位が用いられます。
Point
1ノット(KN、knot)= 1海里/時間
自動車の時速とは単位が異なるだけで、時間、距離、速力の関係は全く同じです。相互の関係は、以下のようになります。
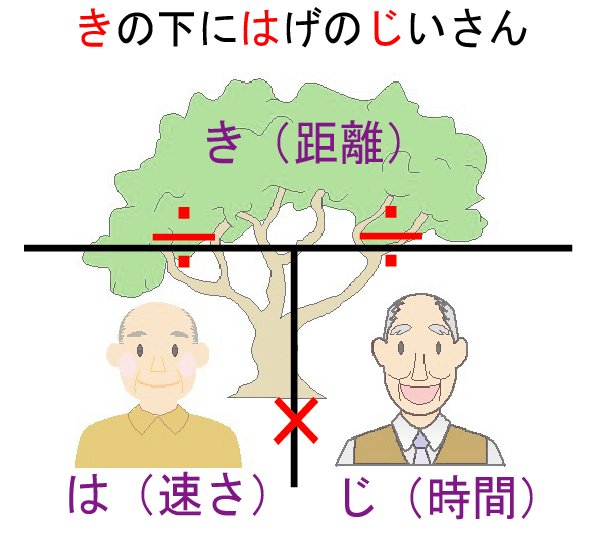
Point
速力(KN)= 距離(NM)÷ 時間(h)
距離(NM)= 速力(KN)× 時間(h)
時間(h) = 距離(NM)÷ 速力(KN)
相互の関係は難しくないのですが、少々バカバカしく、図のように丸覚えすることもできます。「木の下にハゲの爺さん」と語呂合わせで覚えます。「きはじ」や「はじき」と丸覚えしても構いません。なお、式中の時間は単位が「時」であるので、「分」は「時」に直しておく必要があります。
Point
分 ÷ 60 = 時 (例)45分 ÷ 60 = 0.75時間
時 × 60 = 分 (例)0.8時間 × 60 = 48分
| 問題 | 式 | 答え |
|---|---|---|
| 35海里を 2時間30分で航海したときの速力 | 35 ÷ 2.5 = 14 | 14ノット |
| 速力 8ノットで 1時間 15分航行したときの航行距離 | 8 × 1.25 = 10 | 10海里 |
| 19.5海里を 13ノットで航行したときの航行時間 | 19.5 ÷ 13 = 1.5 | 1.5 = 1時間 30分 |
| 2004年 8月16日 初版 |
Copyright(C) AOKIDS All Right Reserved.
Top > Others >> 元の位置に戻る >>> 経度、緯度について詳しく
| Boat & Fishing / AOKIDS Home Page |